A Model of Diffuse Broadband Solar Irradiance for a Cloudless Sky
Abstract
An analytic model is presented for the broadband diffuse irradiance received at the earth’s surface through a cloudless homogeneous atmosphere containing light absorbing agents and isotropic scattering agents. The model is extended to include a contribution from light re-scattered after ground reflection.
Thus….
![]()
where S is the diffuse irradiance,
the constant k represents the concentration of intercepting agents:
ka represents absorbers and ks the isotropic (multiple) scatterers so k = ka + ks .
a scattering ratio, D, is defined as ks / k.
Q represents the top of atmosphere irradiance (being the solar constant, Q ~1367 W/m2 ) and
n the zenith angle of the sun and set the vertical coordinate as y, with y = 0 at the ground and y = H at the top of the atmosphere
β . 1.66 and
the albedo is A.
Sometimes the term Transmittance, Tz, is used instead of kH. The relationship is simply exp(-kH) = Tz.
How well does it work? – the figure below shows that it works quite well.
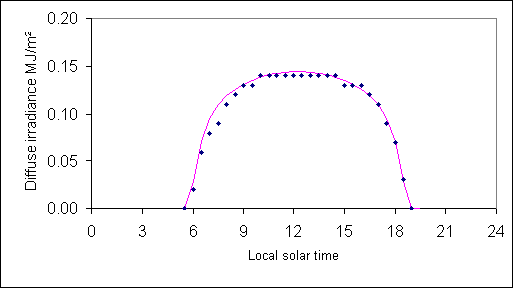
Figure Half-hourly exposures of observed and modelled diffuse irradiance
in MJ/m2 (on a horizontal surface) at
Observed denoted by diamonds, model estimates shown by solid line.
If zenith transmittance Tz which is defined as exp(-kH) is assumed known (say ~ 0.75 being a typical value), then rough estimates of the proportion of scattering agents to intercepting agents (say D ~ 0.5) and Albedo (say A ~ 0.2) provide the input parameters for the analytic model (as expressed by Equation 14). The model then provides simple expression to estimate clear sky diffuse irradiance for any desired zenith angle, n. In this case, the formula reduces to
![]() .
.
In summary, the model provides a simple analytic theory and expression to explain or to estimate broadband diffuse irradiance.